Thevenin's theorem states that
"Any two-terminal linear electrical dc network containing voltage sources, current sources, and resistances can be replaced by an equivalent circuit consisting of only a voltage source (called Thevenin's voltage) in a series connection with a resistance (called Thevenin's resistance).
Applications of Thevenin's theorem
Thevenin's Theorem has many different uses. It can be used in:
- The analysis of electrical circuits consisting of neither parallel nor series sources.
- Reducing the number of components of the electrical circuit and creating an uncomplicated small circuit with the same characteristics.
- Studying the effect of changing an element of the electrical circuit on the behavior of the total circuit without the need to fully analyze that circuit.
Analyzing electrical circuits by using Thevenin's theorem
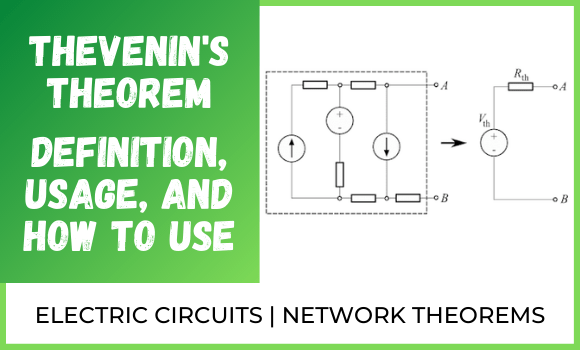
To analyze electrical circuits using Thevenin's theorem, we must find the equivalent Thevenin's circuit, which consists of only a voltage source called Thevenin's voltage in series with a resistance called Thevenin's resistance, as shown below.
Using Thevenin's theorem to find the current through or the voltage across an element or branch
When using Thevenin's theorem to find the current through or the voltage across an element or branch, we follow the following steps:
- We determine the points 'a' and 'b' between the two ends of the element for which the current or voltage is to be found.
- We remove the element for which the current or voltage is to be found (the element between points a and b) as shown in the figure:
- To calculate the value of Thevenin's resistance, we remove all sources by substituting them with their internal resistances (since the internal resistance of the voltage source = zero, it is replaced by a Short Circuit, and since the internal resistance of the current source = infinity, it is replaced by an Open Circuit). Then we suppose a current passes from point a and returns to point b.
- To find the value of Thevenin's voltage, we return the removed sources, and then calculate the value of Thevenin's voltage between points a and b which in this case is equal to the voltage of R2 as shown in the figure:
- We draw Thevenin's circuit and place the element which was removed in step 2 between points a and b in Thevenin's circuit as shown: