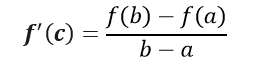[Summary] Mean-Value Theorem

Mean-Value Theorem states that:

if a function " f " is 

1. Continuous on the closed interval [a, b] 
2. Differentiable on the open interval ]a, b[ 

then, there is at least one value c ∈ ]a, b[ so that:

 

How can you  find the value of  "c"?

1. Make sure that the function " f " satisfies the conditions of Mean-Value Theorem
2. Find  f′(x) (The derivative with respect to "x")
3. Put  f′(c) (We replace the "x" in the derivative with "c")
4. Find  f(b) & f(a)
5. Find "equ "
6. Equal the results of the third and fifth steps to find the value of "c"