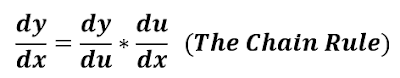The Chain Rule for Derivative

What is the Chain Rule? 

It is a mathematical formula for calculating the derivative of composite functions such as f (g(x))

 

If we have two functions:

Y = f (u) , u = g (x)

[ The two preceding functions can also be expressed as f (g(x)) ]

Then

[The derivative of "y" function with respect to x (dy/ dx) = The derivative of "y" function with respect to u (dy/du) Multiplied by the derivative of "u" function with respect to x (du/dx) ]

Steps to find the first derivative of a composite function using the Chain Rule:-

1. Find y ′ [The derivative of y function with respect to u (dy/du) ].
2. Find u ′ [The derivative of u function with respect to x (du/dx) ].
3. Multiply the two derivatives.
4. Substitute for the value of u.
5. Substitute for the value of x -if any.

Example

Use the Chain Rule to find the first derivative of the following function when x=3:-
 

Solution:-

1- We rewrite the function y with respect to u (we form two functions. The first function is the function "y" with respect to u, and the second function is the function "u" with respect to x). In this problem we will impose what is under the square root with u.

2- Find y ′ [The derivative of "y" function with respect to u (dy/du) ]

3- Find u ′ [The derivative of "u" function with respect to x (du/dx) ]

4- Multiply the two derivatives

5- Substitute for the value of u

6- Substitute for the value of x