Finding the Maximum & Minimum Values of a function (First Method)

How the maximum and minimum values of a function can be found?

We can find the maximum and minimum values of a function by using the first derivative  y':

 

If the function " f " is:-

1. continuous on the closed interval [a, b] 
2. derivatable on the open interval ]a, b[ 
3. c ∊ ]a, b[

Then, there are two cases:-

Case 1

 

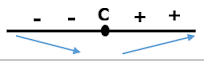
In this case, function f  has a local maximum value at c, its coordinates (C, F(C))

 

Case 2

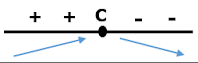
In this case, function f  has a local minimum value at c, its coordinates (C, F(C)) 

 

Note:-

The previous theory remains true if f'(x) does not exist. However; f(x) is connected at x=c

 

How to find the maximum / Minimum values of a function using the first derivative y':

1. We find f ′ (x) (the derivative with respect to "x")
2. We put f ′ (x) = 0 (we find the derivative roots)
3. We study the derivative signal before and after its roots, and there are 4 cases:

 

The Case (around x=c)	What does it mean
	The function f has a local minimum value, at x = c, its coordinates are (c, f (c)).
	The function f has a local maximum value at x = c , its coordinates are (c, f (c)).
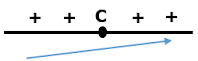
	The function f has no maximum nor minimum values (The function is increasing on its domain)
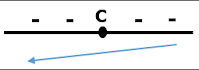
	The function f has no maximum nor minimum values (The function is decreasing on its domain)

 

Notes

1. The monotonic function is a function which is either entirely increasing or decreasing on its domain.
2. If f (x) is:-
• a function defined for the period [a, b]
• has a local maximum or minimum value at x = c where c ∊ ] a, b [
  Then, if f´ (c) is known then f´ (c) = 0
3. Sometimes f´ (c) may equal 0 (f´ (c)=0). However; the function f has no maximum nor minimum values at x = c (the function is monotonic)