[Summary] How Poles' Locations Affect The System's Response

Poles' locations on the S-plane determine the type of the system's transient response and therefore determining its stability. In this article, I will discuss the three possible locations of poles on the S-plane, and how they affect the system's response.

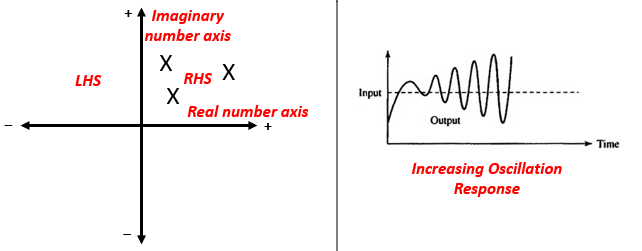
By the way, the "S-plane" is a two-dimensional space delivered by two orthogonal axes, the real number axis and the imaginary number axis. Therefore; a point in the S-plane represents a complex number.

S-plane

Case 1: All the poles are located on the left hand side of the S-plane

In this case, the system gives a stable time response, and there are  two sub-cases:

1. All the poles are pure real numbers (not complex numbers).
   In this case, the system's response is of the type "overdamped response" or "critically damped response". 
   
   
   
   
   Note: The distance from the origin of the S-plane to the pole is inversely proportional to the rise time of the response, that is, the greater the distance, the less the rising time of the response, and therefore the faster the response is.
   
   
2. All the poles are complex numbers (consisting of real and imaginary parts).
   In this case, the system's response is of the type "underdamped response"
   
   

Notes: 

• The distance from the origin of the S-plane to the pole is directly proportional to the natural frequency of the transient response.

• The ratio of the real part to the imaginary part is related to the amount of damping. The higher the real part relative to the imaginary part, the faster the damping is.
  
  
• Always, the poles located closer to the origin of the S-plane are the ones that determine and control the nature of the system's response. Therefore; They are called "the dominant poles".

Case 2: All the poles are located on the imaginary axis of the S-plane.

In this case, the system gives a Quasi-stable time response of the type "constant oscillation response" which we consider it as an unstable response in Automatic Control Systems. 

Case 3: All the poles are located on the right side of the S-plane.

In this case, the system gives an unstable time response, and there are two sub-cases:

1. All the poles are pure real numbers (not complex numbers).
   In this case, the system's time response is of the type "exponential rise response"
   
   
   
   
2. All the poles are complex numbers (consisting of real and imaginary parts).
   In this case, the system's response is of the type "increasing oscillation response"
   
   

*****This Summary is available as PDF File 

Click here to get a PDF Copy*****