[Summary] Learn How to Draw Root Locus in Just 10 Minutes

What is Root Locus?

Root Locus is a graph sketched on the S-plane that shows the path taken by the poles in the closed system when the value of K (gain) changes from zero to infinity. Because when the value of K changes, the values ​​of the zeros remain constant while the values ​​of the poles change thus changing the stability of the system. To know how the values of poles affect the system's stability. Click here

What is Root Locus used for?

It is used for studying and improving the stability of the system.

How to draw Root Locus?

1. We determine the number of poles (Np ), the number of zeros (Nz ), and the number of asymptotes (NAsymptotes).
   Knowing that:
• The poles are the roots of the denominator.
• The zeros are the roots of the numerator. 
• NAsymptotes = Np - NZ 
  
  
2.  Based on the number of asymptotes, we determine their shapes as follows:
   

   

   Shapes of Asymptotes based on their numbers

   
   
3.  If we have two or more asymptotes, then we must find the point of their intersection using the following equation:
   

   

   The equation to find the point of intersection of asymptotes

   
   
   NOTE: When summing poles, if the poles are complex numbers, we take the real parts only because the imaginary parts always cancel each other when adding them.
   
   
4. We draw the Root Locus as follows:
• Draw the S-plane.
• Locate the zeros and represent them by empty circles "O", and locate the poles and represent them by "X" signs.
• Draw the asymptotes - according to the information obtained from steps 2 and 3, on the S-plane.
• Determine the locations in which the locus occurs and those where it doesn't occur as follows:
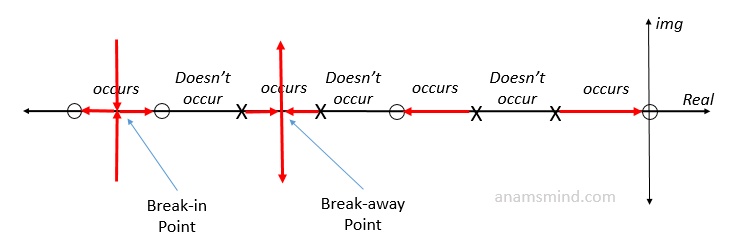
  We start from the first pole or zero from the far right, and then follow the following sequence: It occurs, it doesn't occur, it occurs, it doesn't occur, and so on, as shown below:
  
  

• Only draw the locus line on the locations where it occurs, knowing that the locus line always comes out from the pole and goes towards the zero (by the zero here we means the roots of the numerator, not the zero of the S-plane), or goes towards infinity if there are no zeros left and in this case makes an asymptote.
  
  There are three cases for the locus line

• Case 1: If we have a pole and a zero
• Case 2: If we have two poles (a break-away point is formed) 
• Case 3: If we have two zeroes (a breaking-in point is formed) 

How to draw Root Locus in MATLAB?

To draw Root Locus in MATLAB insert the following Code: